EKB-20250728-滑動螺桿傳動效率計算-Sun

A238

114.10.20

114.09.30

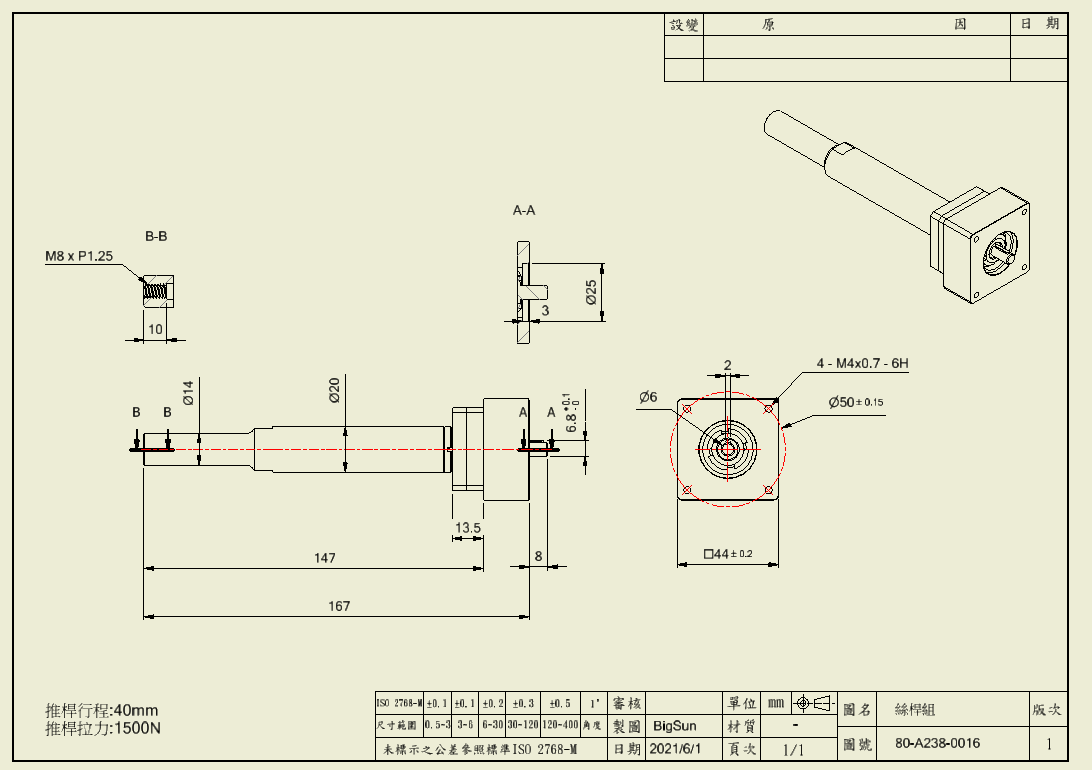
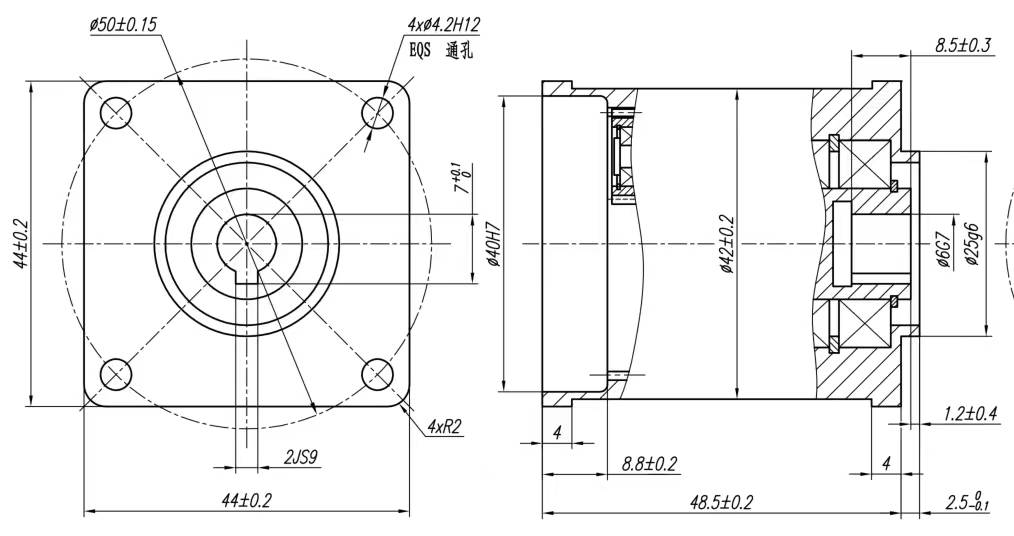
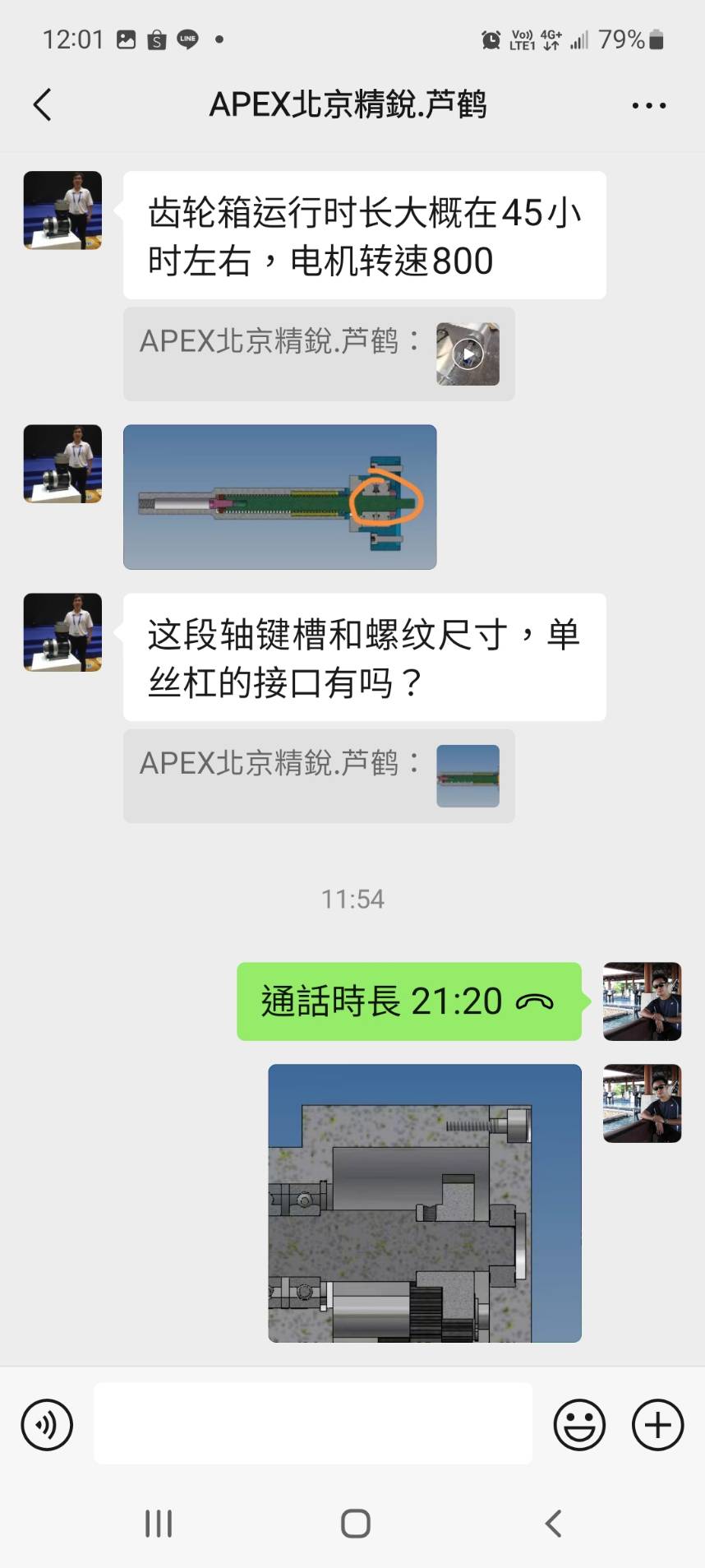
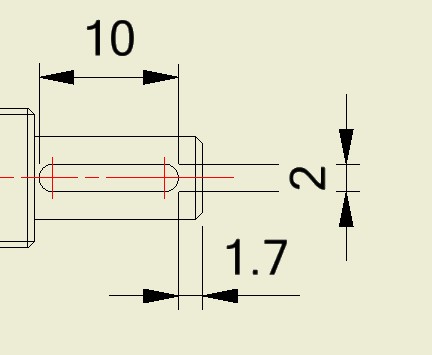
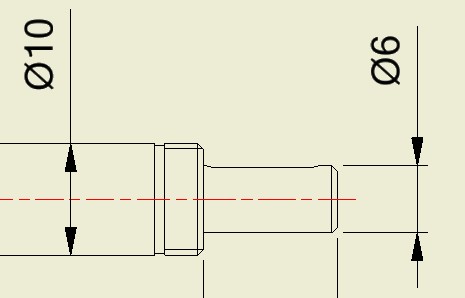
減速箱尺寸

114.09.28

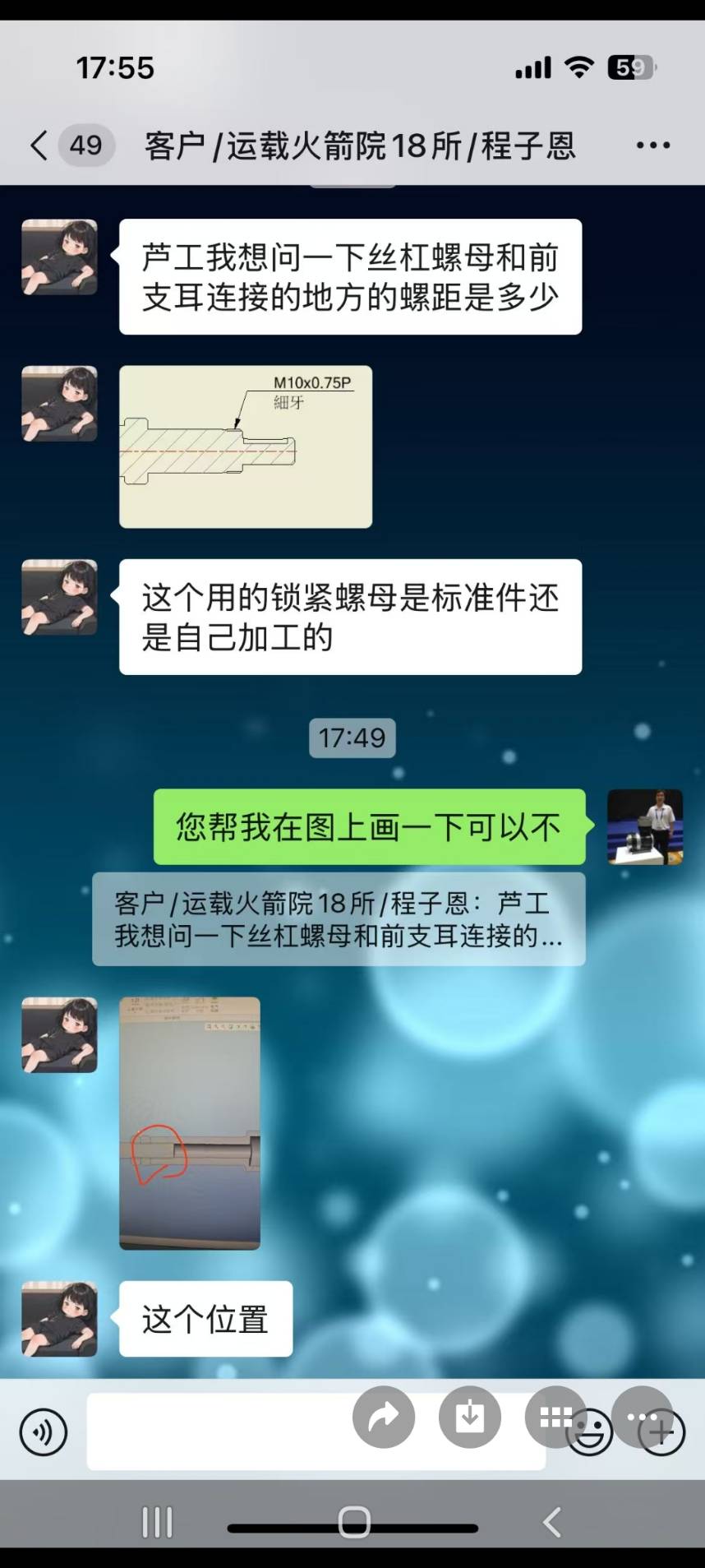
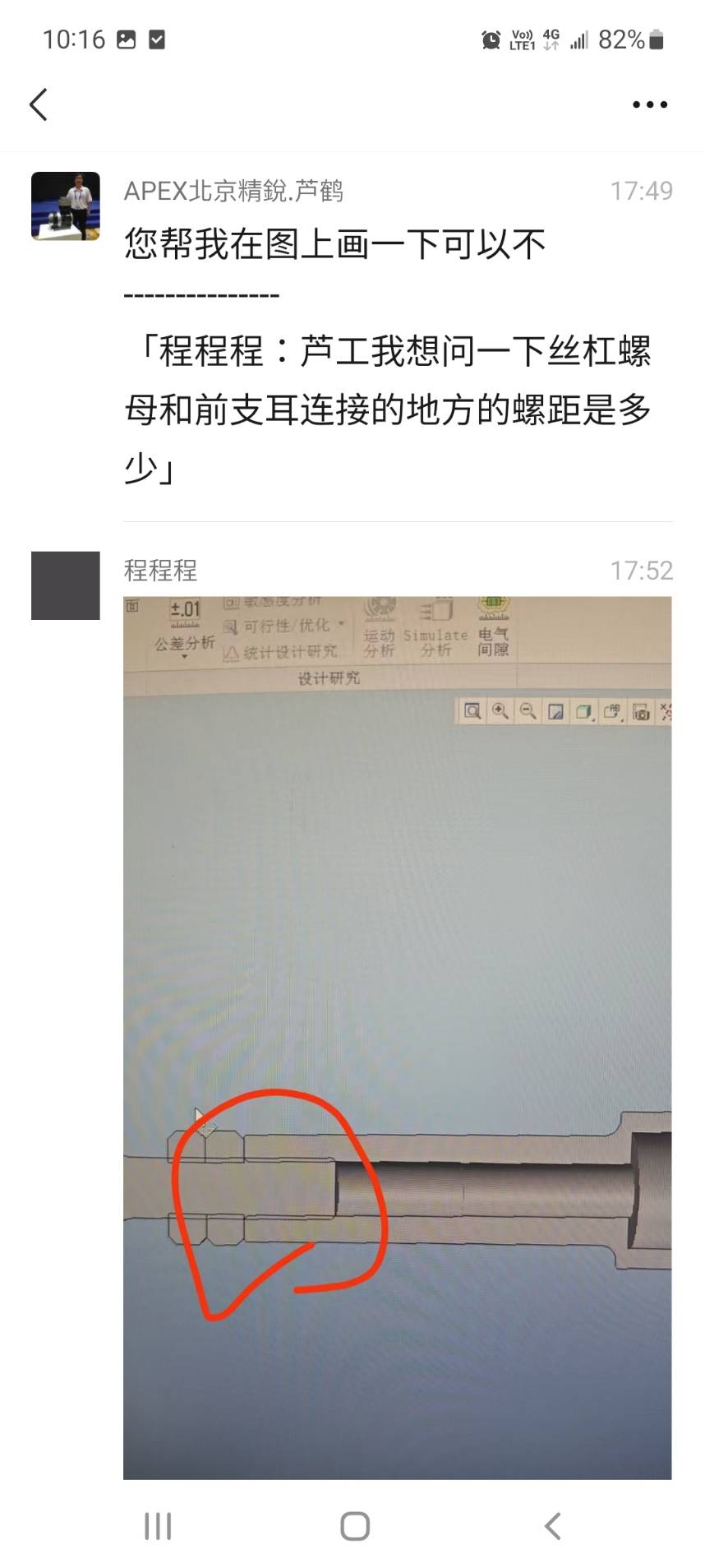
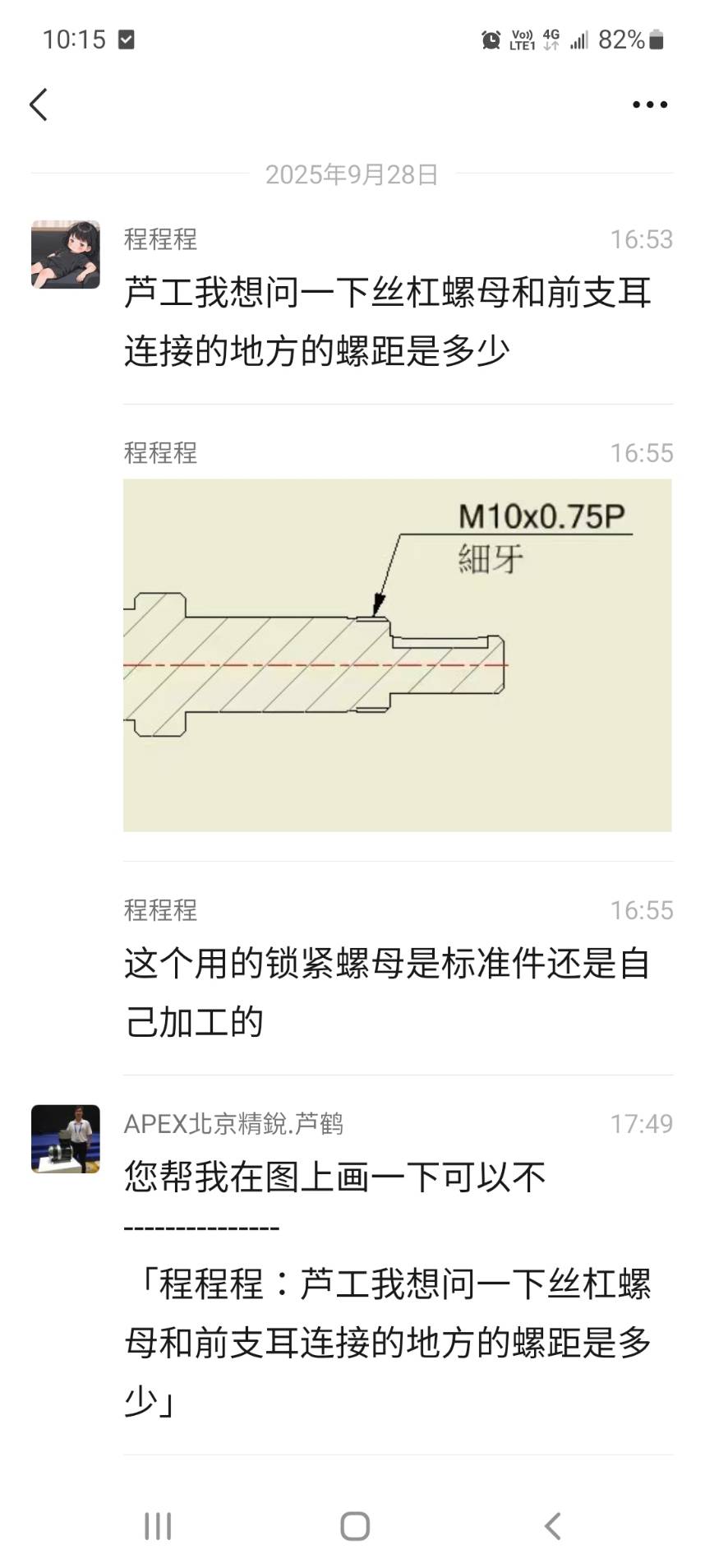
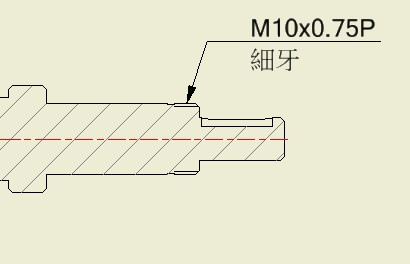
1. 鎖緊螺母是標準件

2. 前耳螺距

114.09.26

114.07.28

A238

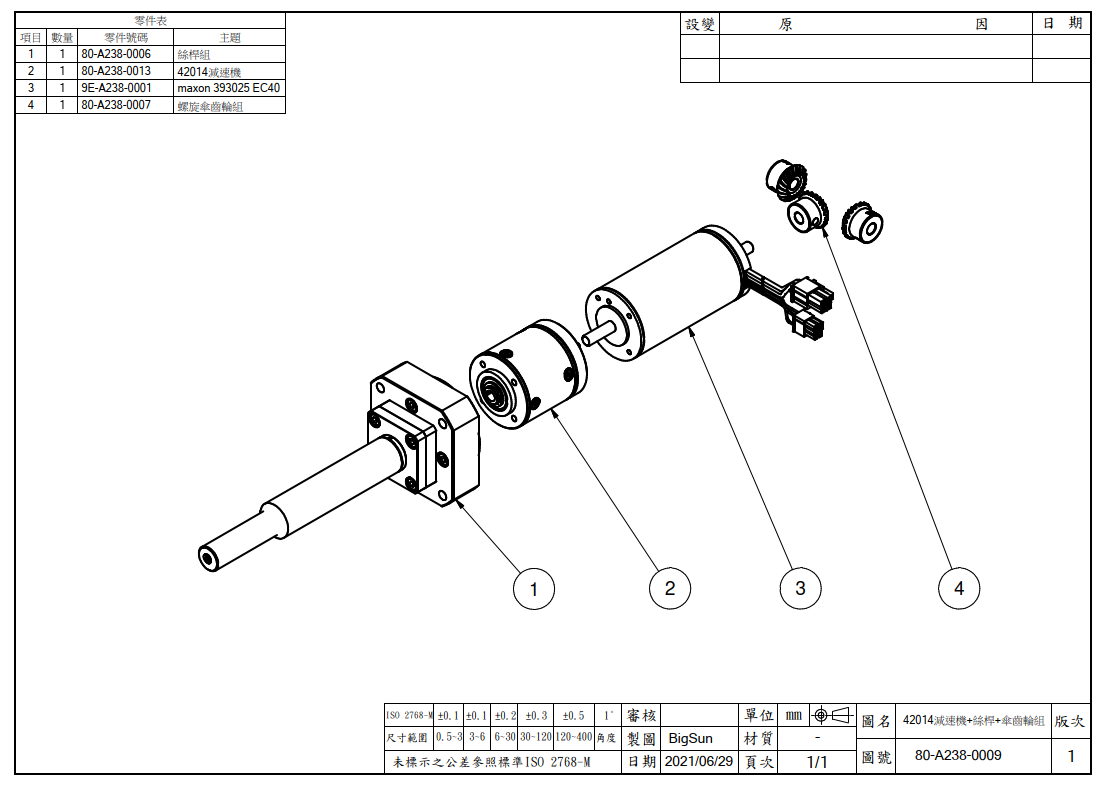
傳動總效率

90% X 42% = 37.8%

雙層行星減速機效率

95% X 95% = 90%

滑動螺桿效率

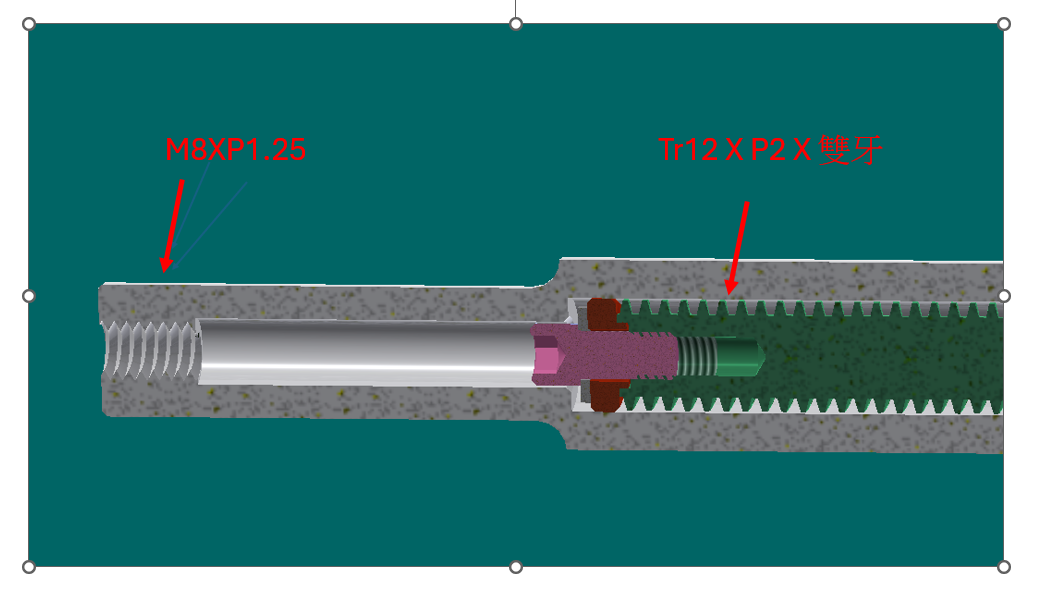
Tr12 x P2 雙牙梯形螺桿的傳動效率約為 42%

已知參數

• 螺紋規格：Tr12 x P2 雙牙

  • 螺桿公稱直徑 $d = 12 , mm$

  • 螺距 Pitch $P = 2 , mm$

  • 雙牙 (2-start) → 導程 $L = 2 imes 2 = 4 , mm$

• 螺桿有效牙長：78 mm（影響摩擦距離）

• 假設螺帽材質為青銅，摩擦係數 $mu = 0.15$

• 假設有效螺紋接觸角 $phi = 0^circ$（即未考慮摩擦角度的影響）

  梯形螺桿效率估算公式

  對於不自鎖的梯形螺桿，其效率 $eta$ 可估算為：

  $$eta = rac{ an lambda}{ an (lambda + phi)}$$

  其中：

  • $lambda$：導程角

  • $phi = an^{-1}(mu / cos alpha)$，α 是螺紋半角，對於梯形螺紋，α ≈ 15°

    
    

    ① 導程角 λ 計算：

    $$an lambda = rac{L}{pi cdot d_m}$$

    • 導程 $L = 4 , mm$

    • 中徑 $d_m = d - rac{H}{2} approx 12 - 1 = 11 , mm$

    $$an lambda approx rac{4}{pi cdot 11} = 0.1158 Rightarrow lambda approx an^{-1}(0.1158) approx 6.61^circ$$

    ---

    ② 摩擦角 φ 計算：

    $$phi = an^{-1} left( rac{mu}{cos alpha} ight) = an^{-1} left( rac{0.15}{cos 15^circ} ight) approx an^{-1}(0.155) approx 8.8^circ$$

    ---

    ③ 傳動效率 η：

    $$eta = rac{ an lambda}{ an (lambda + phi)} = rac{0.1158}{ an(6.61 + 8.8)} = rac{0.1158}{ an(15.41)} approx rac{0.1158}{0.2756} approx 0.42$$

結論：

這支 Tr12 x P2 雙牙梯形螺桿的傳動效率約為 42%。