1. 數據呈現階梯跳躍的物理模型探討:
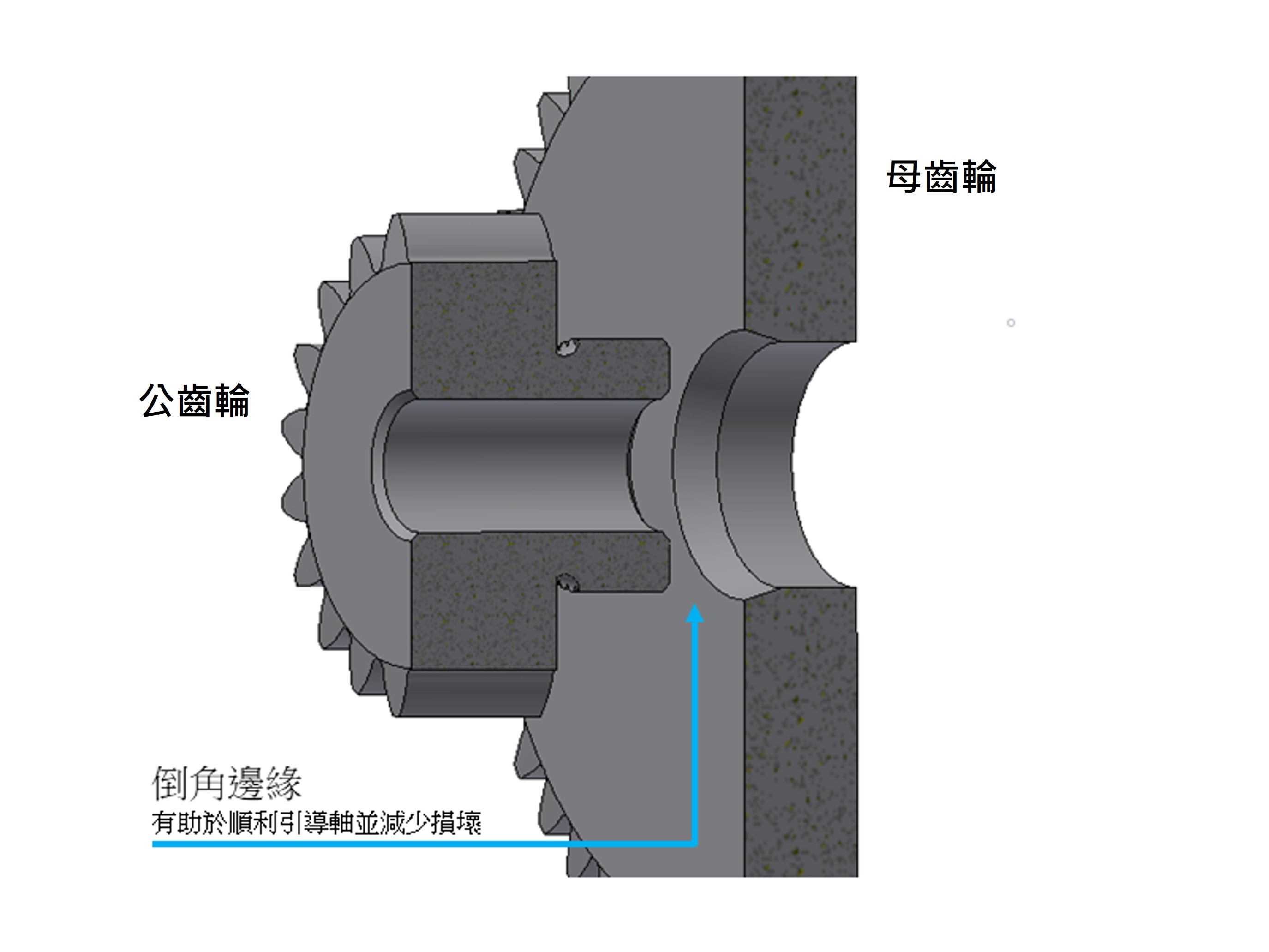
兩個齒輪壓合的過程中，公齒輪插桿跟母齒輪孔洞進行一步步深入嵌合的時候，在每個階段需要加大壓力克服靜摩擦，然後進入大約固定壓力的動摩擦過程，直到推進產生的高溫膨脹累積到一定的門檻，使得頂針跟公齒輪表面阻力大過這個壓合的壓力而無法順利深入，需要進一步加大壓力來克服更高階段的靜摩擦，我們把這樣一個要和過程的關鍵點稱為”關卡”(Critical Stuck Point, CSP)
2. 數據呈現階梯跳躍的模式探討：
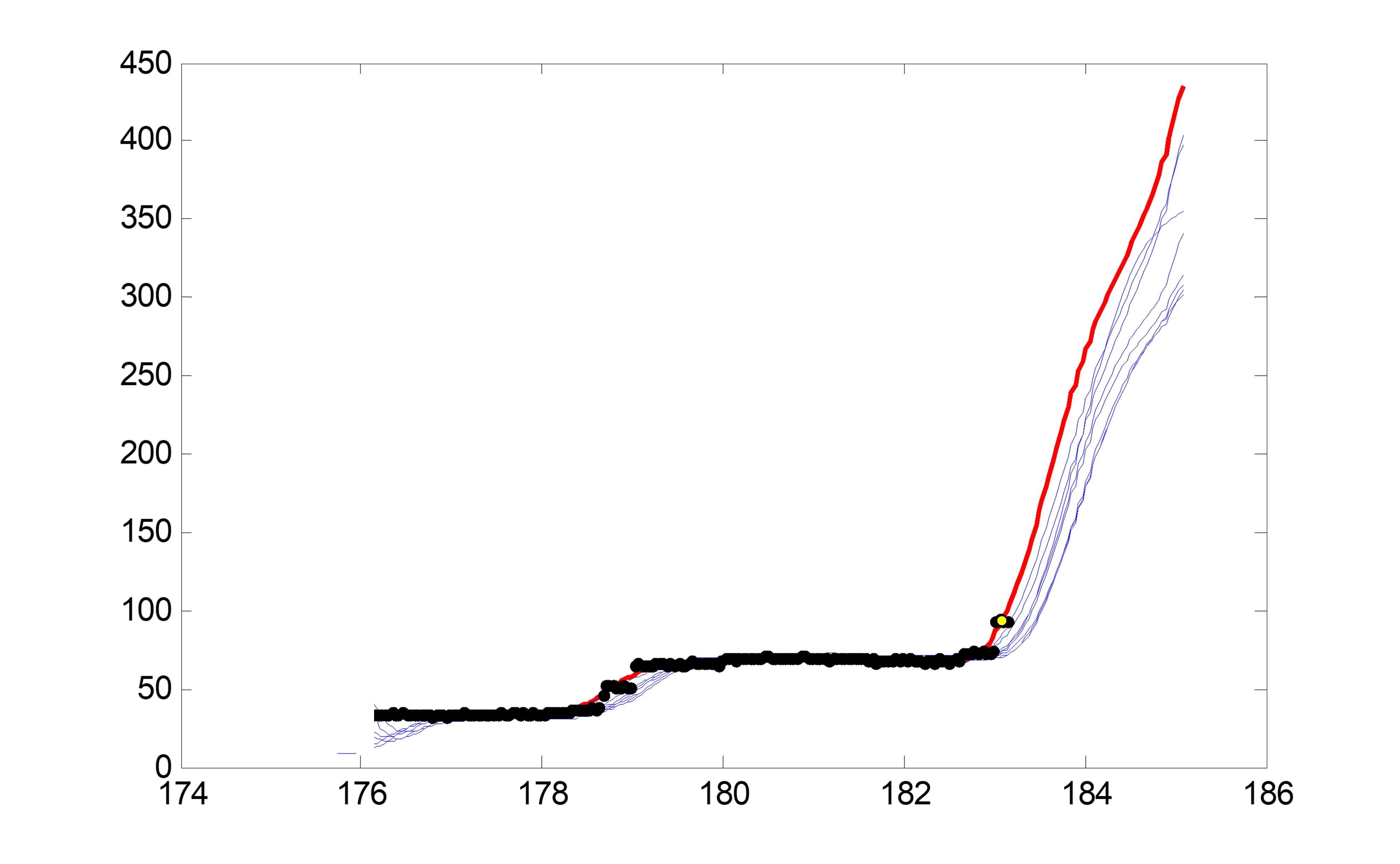
數據的走勢（型號22）可以大致分成三個階段：
- 低阻力階段 (LRS : Low Resistance Stage)
- 中阻力階段 (MRS : Medium Resistance Stage)
- 高阻力階段 (HRS : High Resistance Stage)
這三個階段會分別有不同數量的關卡 (Critical Stuck Point) 跟壓力跳階 (Steps)
- 低阻力階段 (LRS : Low Resistance Stage) -有兩個關卡跟壓力跳階（2 Critical Stuck Point CSPs & 2 Steps) ;
- 中阻力階段 (MRS : Medium Resistance Stage) - 有兩個關卡跟壓力跳階（2 Critical Stuck Point CSPs & 2 Steps) ;
- 高阻力階段 (HRS : High Resistance Stage) - 有六個關卡跟壓力跳階（6 Critical Stuck Point CSPs & 6 Steps) ;
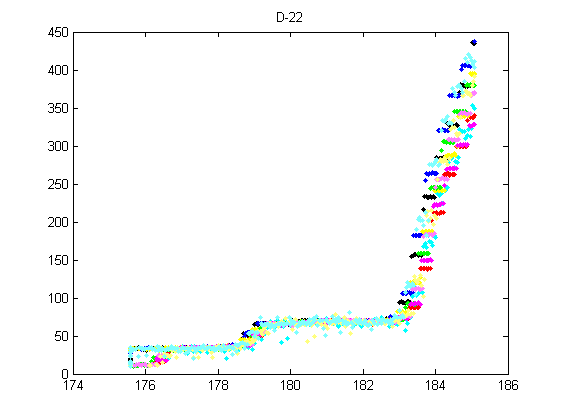
型號32 在高阻力階段(HRS) 有兩組模式（可能因為齒輪原料冶金鑄造或CN C加工鑽孔過程造成的差異）-
這兩組在HRS(高阻力階段)有明顯差異： A組不僅所需的壓力明顯更高，壓力跳躍的階數（關卡數）也不同
A組有 3 個關卡跟壓力跳階
B組有 2 個關卡跟壓力跳階
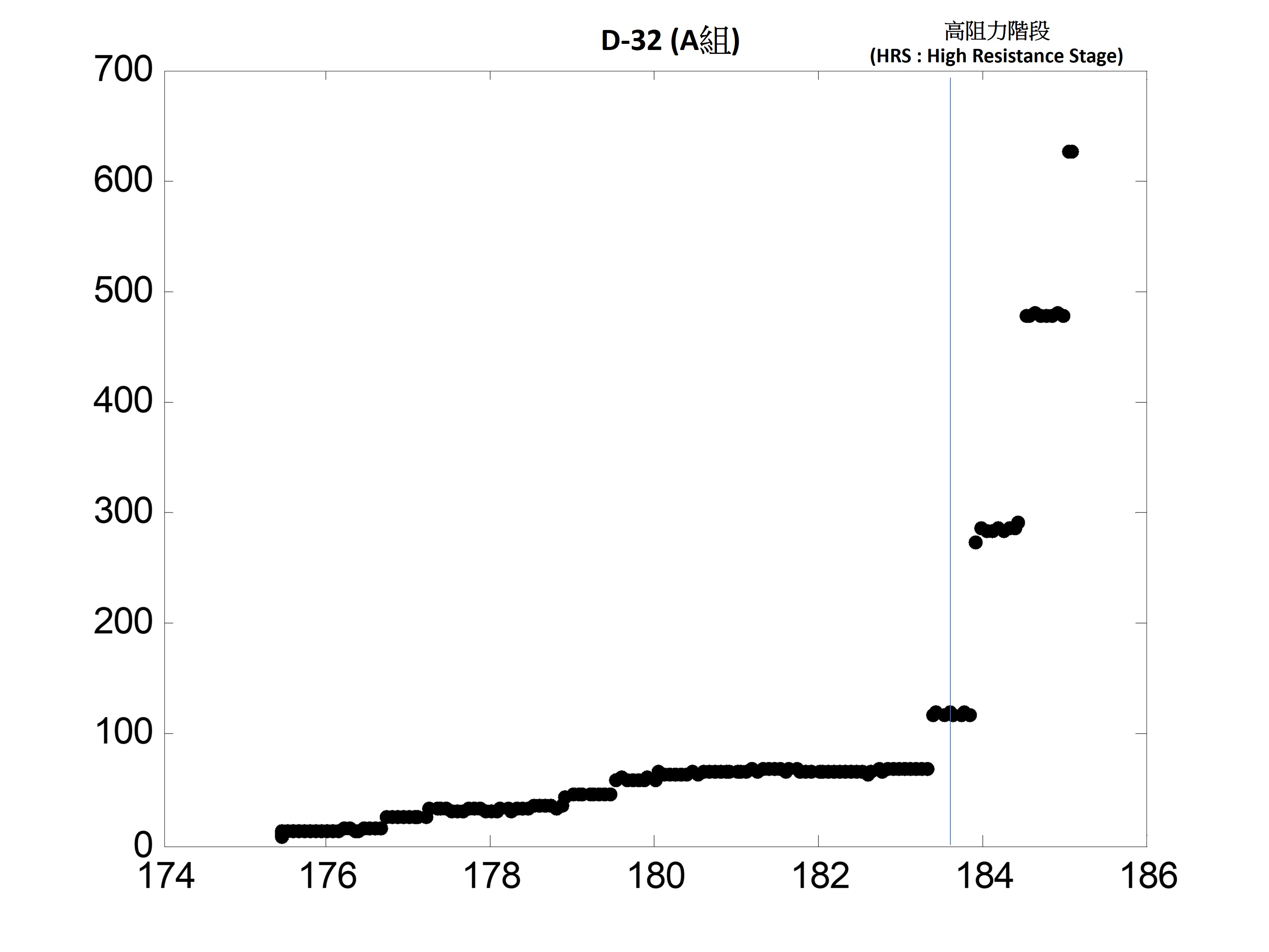
(A組有 3 個關卡跟壓力跳階)
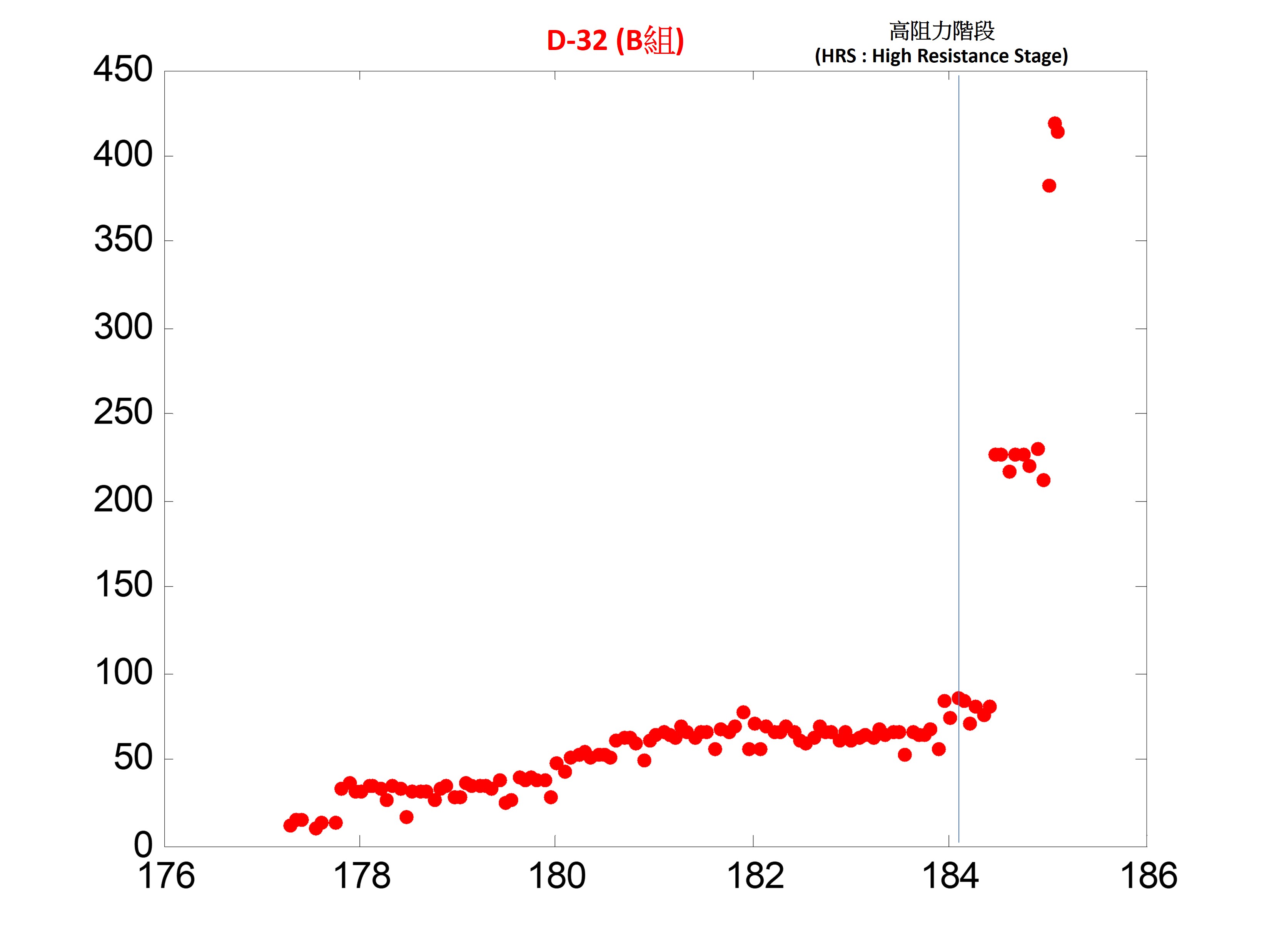
(B組有 2 個關卡跟壓力跳階)
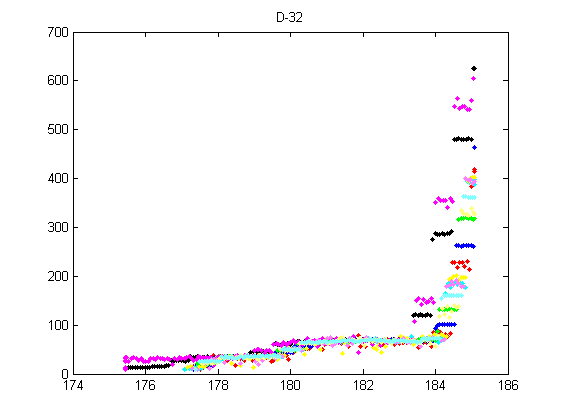
(32齒輪的壓力跳階)
3. 壓合過程預警系統的核心AI適應性回歸（Adaptative Regression) 統計模型：
3.1. 仔細觀察每一組齒輪壓合過程中突破關卡的壓力跳躍數據，我們發現跳點發生的位置跟壓力都不一樣，這些跳躍點在曲線函數分析上是奇異點（Singularity)，必須以最先進的無母數統計模型分析為基礎（詳見鄭振和博士的博士論文, PhD Thesis 2002, Department of Statistics, UC Berkeley)，但由於實驗所提供的樣本數太少(50組)，在這個實驗設計階段，無法詳細分析每一個跳點的統計模式，來得到跳躍點的發生是否正常的信賴區間，但從這些跳躍的規律模式，我們相信如果實驗的樣本數足夠，我們不僅能夠建立精準的統計模型，更可能結合卜瓦松隨機過程(Poisson Process)以及熱力學熱傳導擴散模型/金屬受熱的膨脹張量的有限元素法的推導，得到突破性的工業製造研究成果
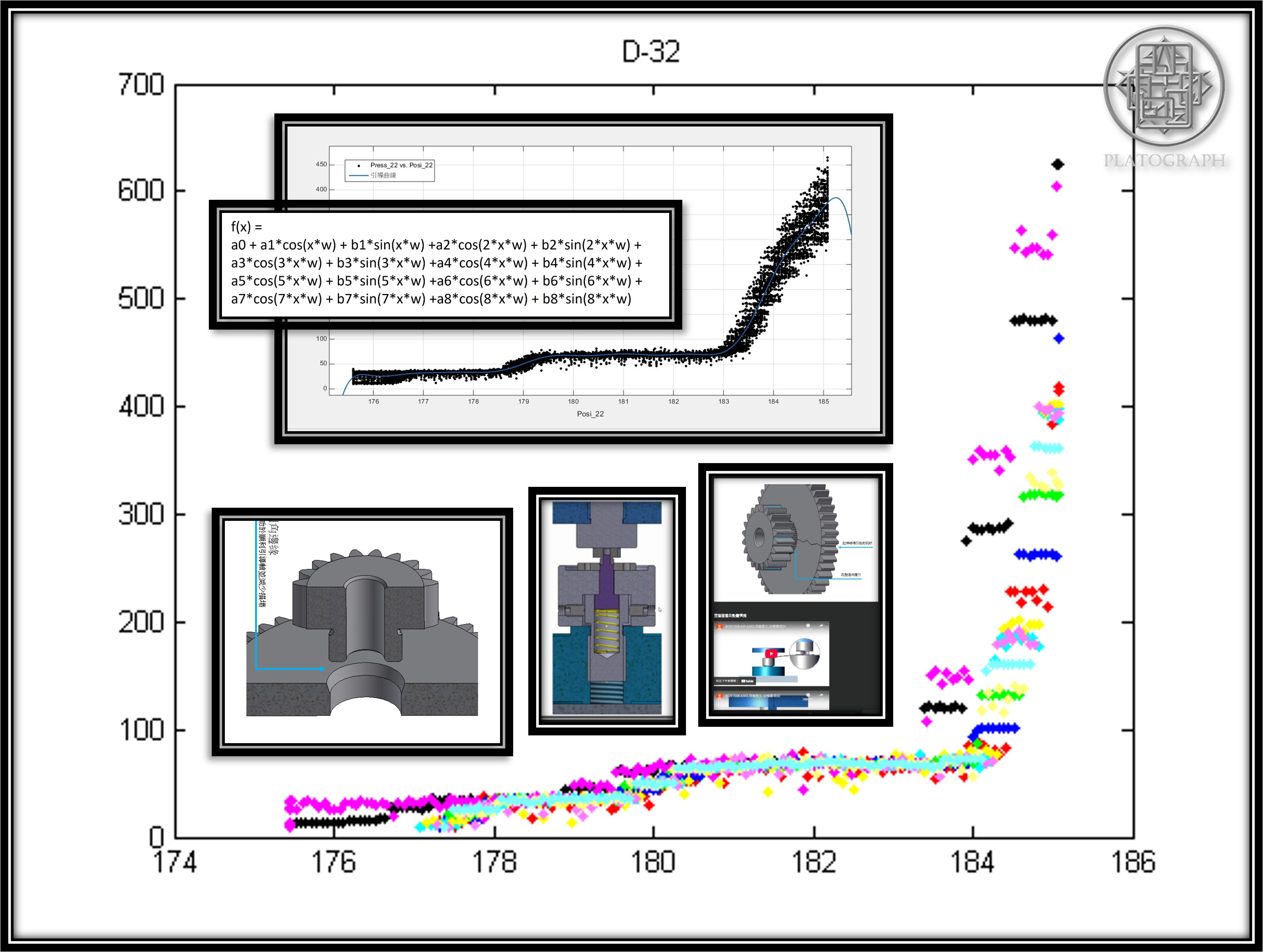
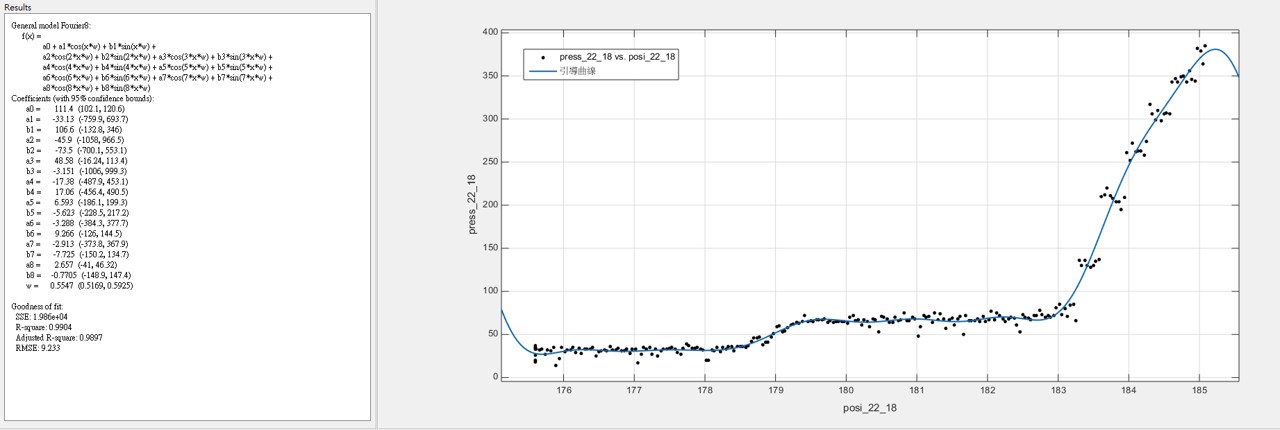
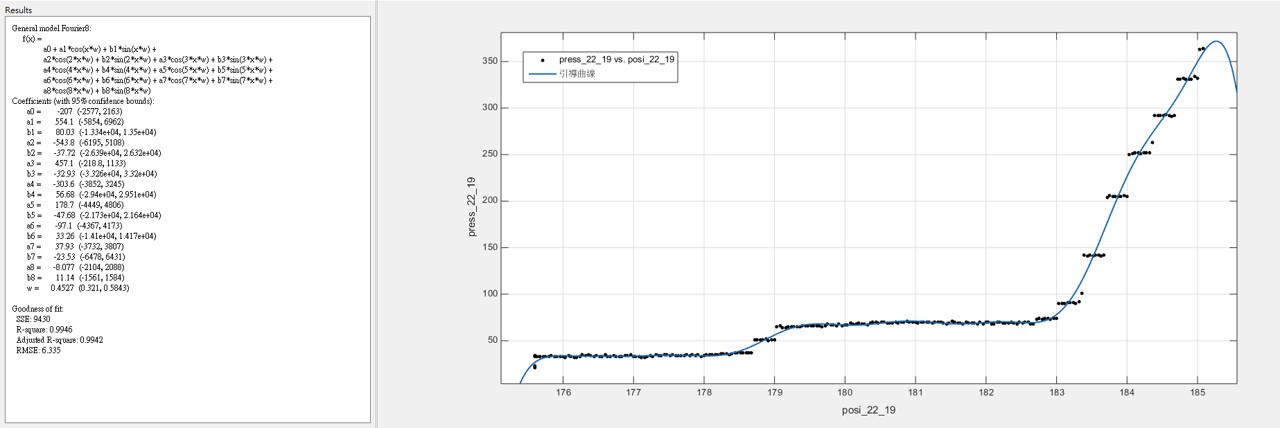
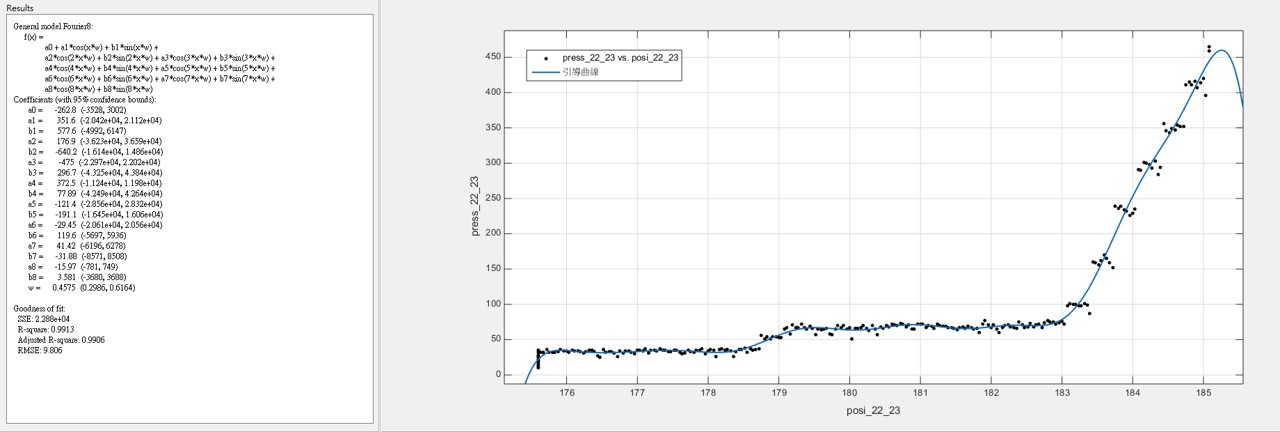
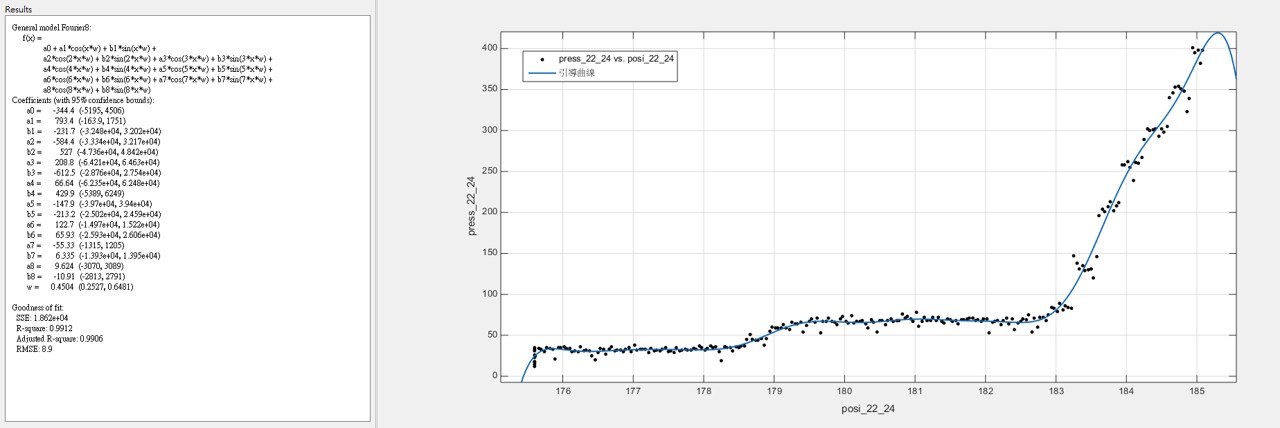
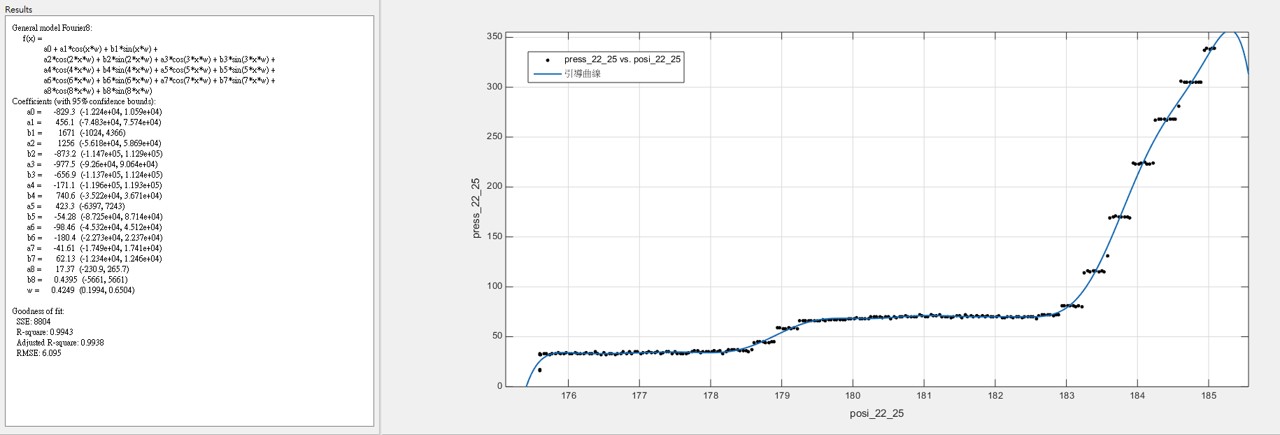
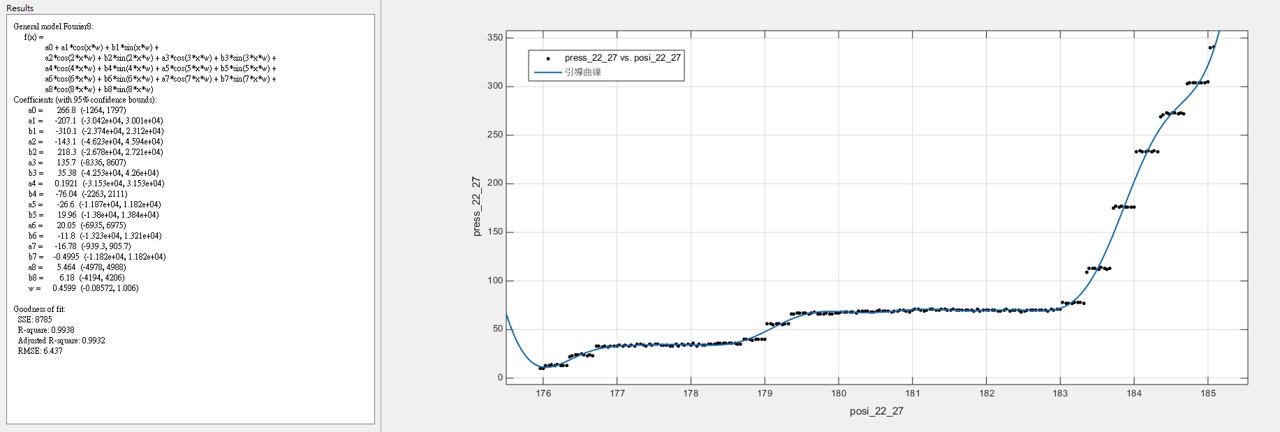
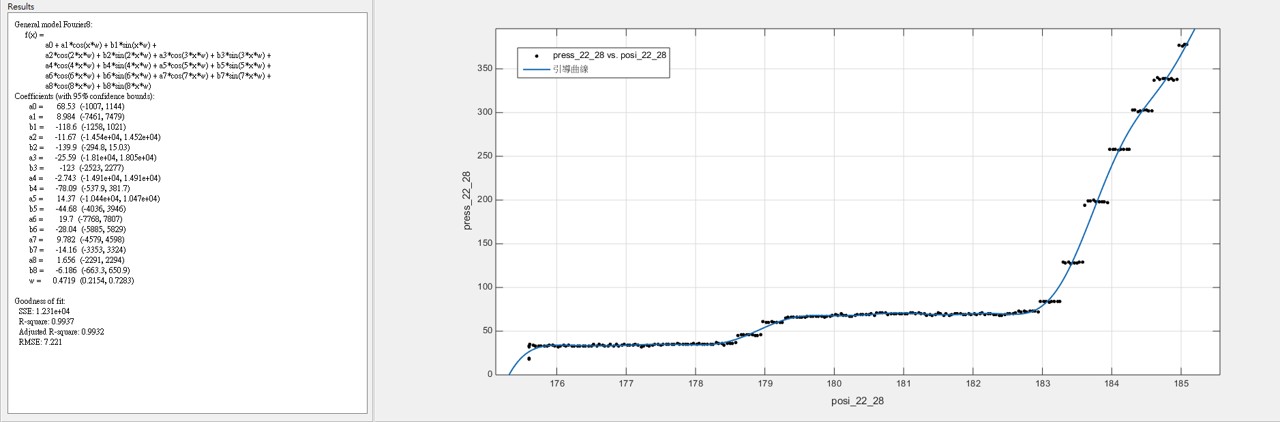
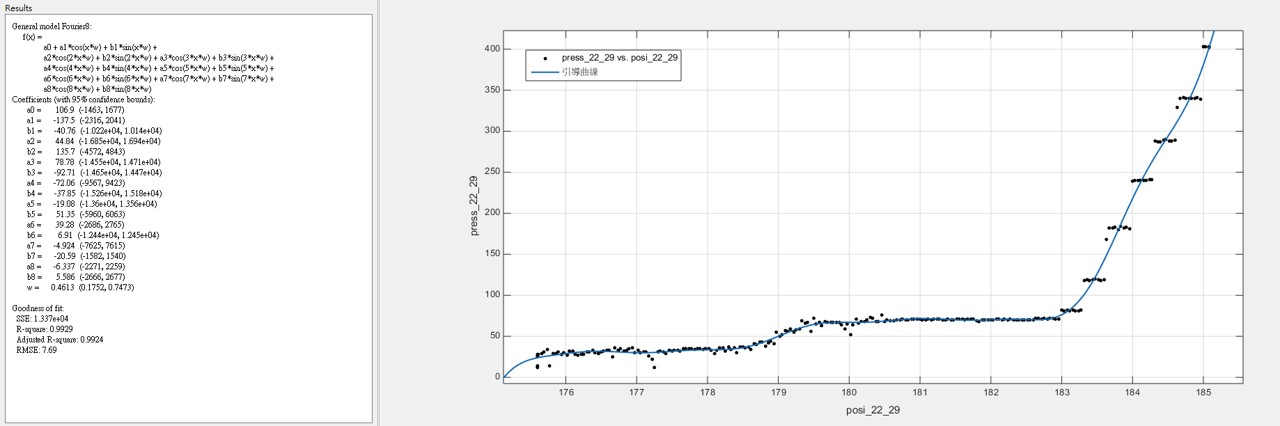
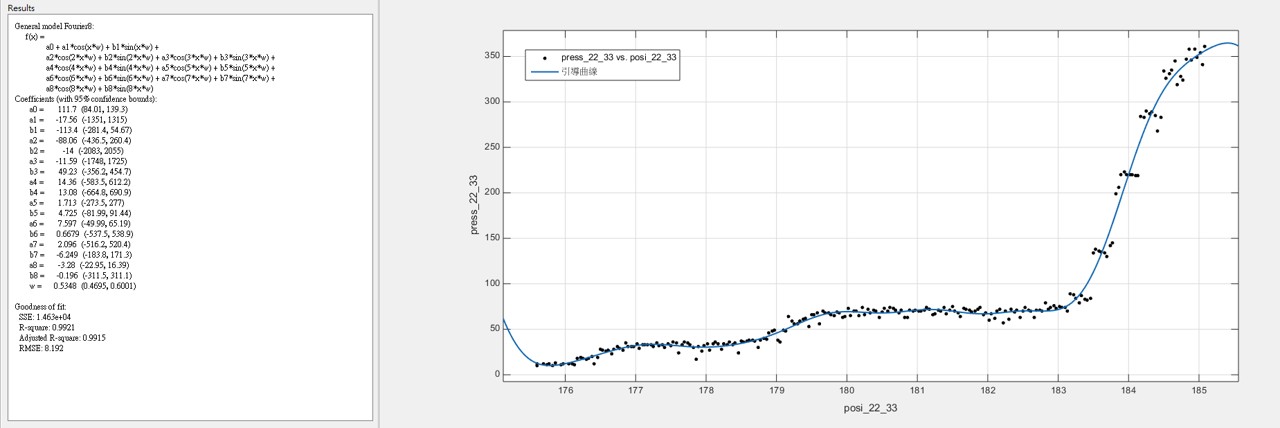
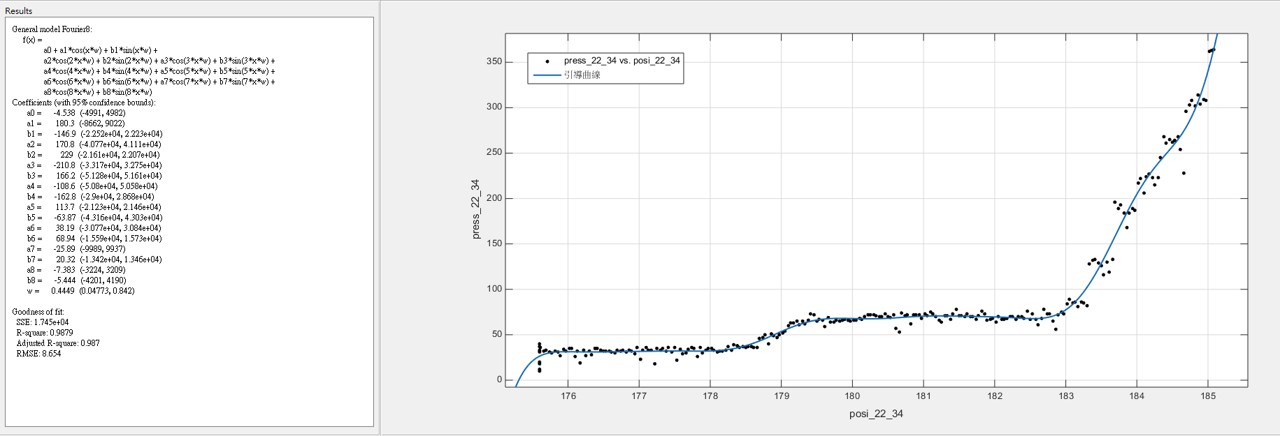
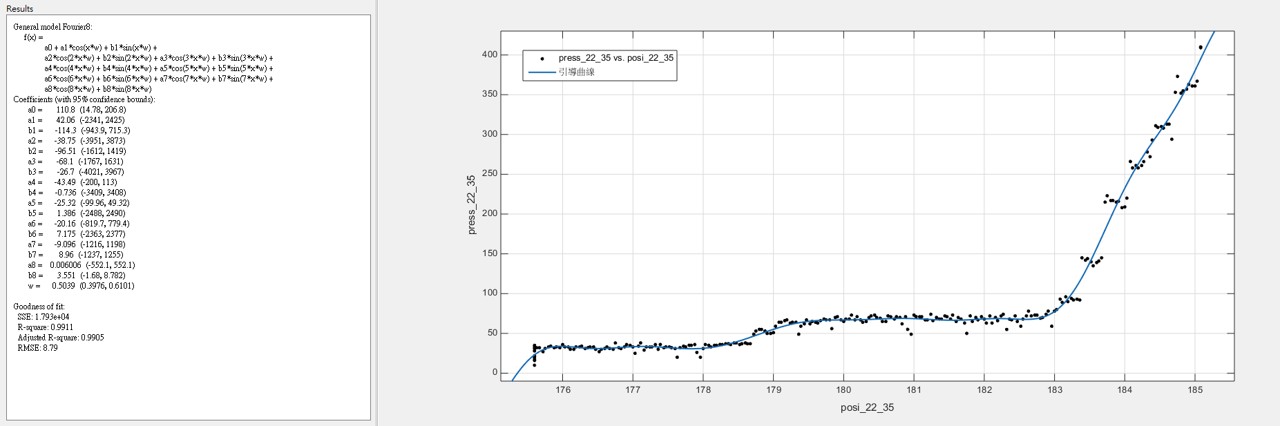
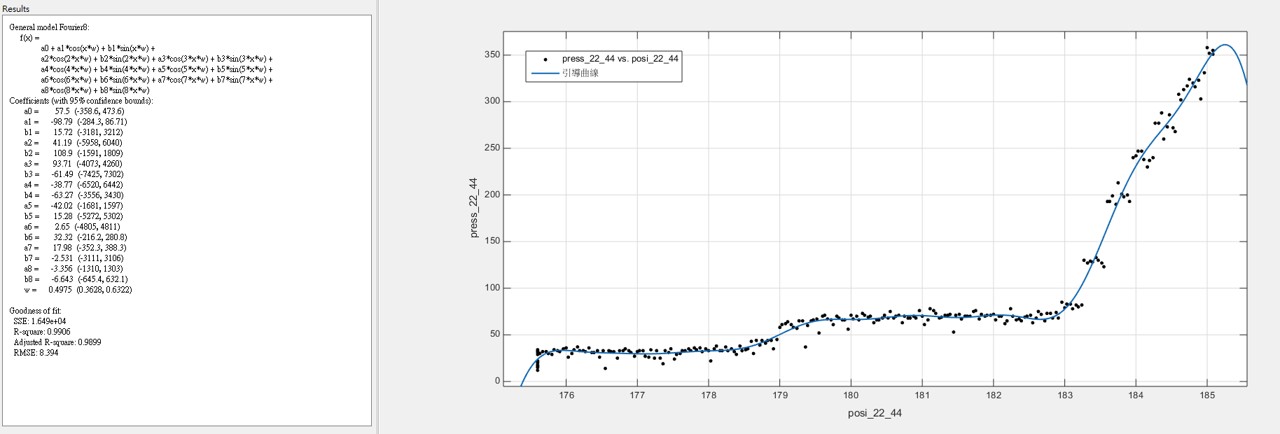
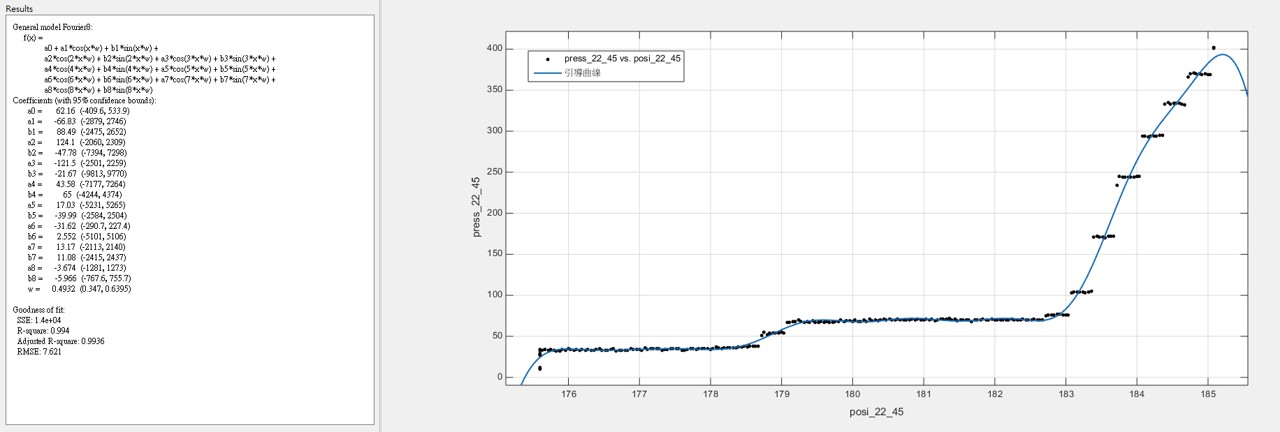
3.2 雖然樣本數不多，根據我們所發現的大概跳躍規律，我們把50組數據統合在一起發現，可以用較為簡單的參數化模型回歸出”引導曲線” - 在眾多的非線性參數化模型中，基於傅利葉分析(Fourier Analysis)的模型，提供最簡潔明瞭的引導參數 ～註：兩百多年前，傅利葉分析方法的發現就是基於傅立葉在金屬的熱傳導研究）
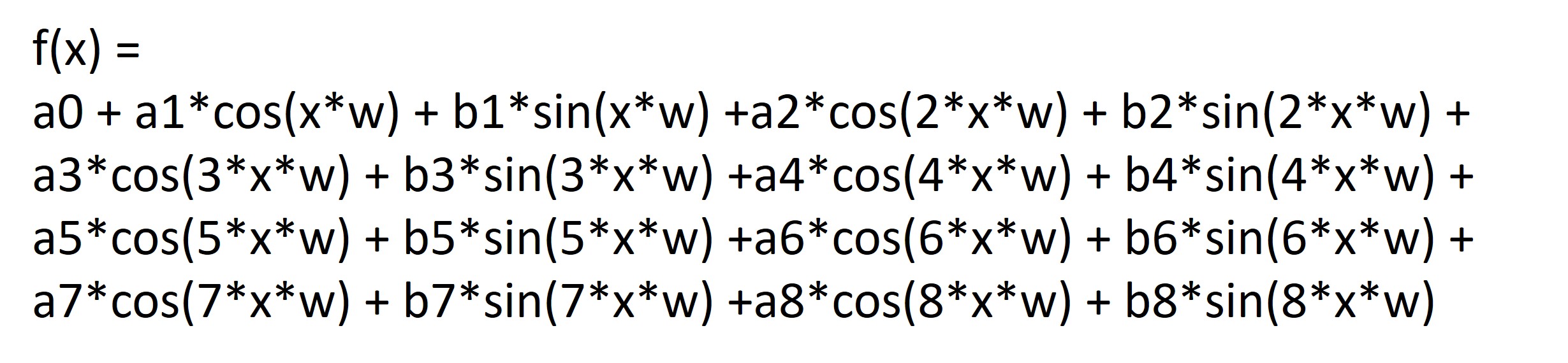
(傅利葉分析的模型)
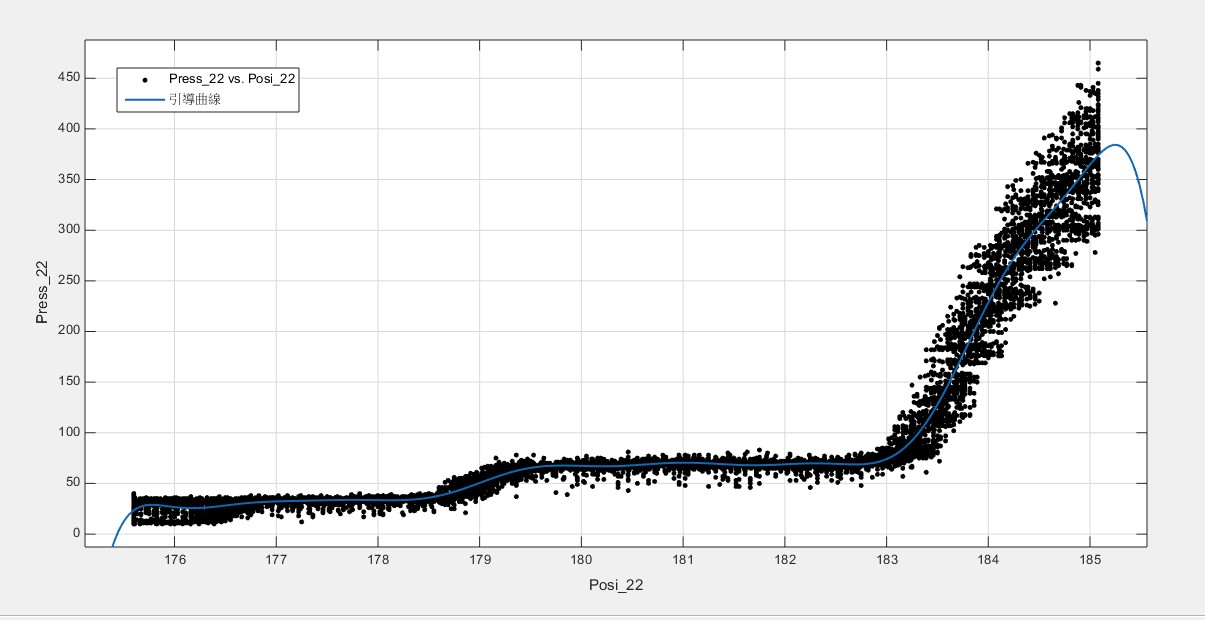(22齒輪的引導曲線)
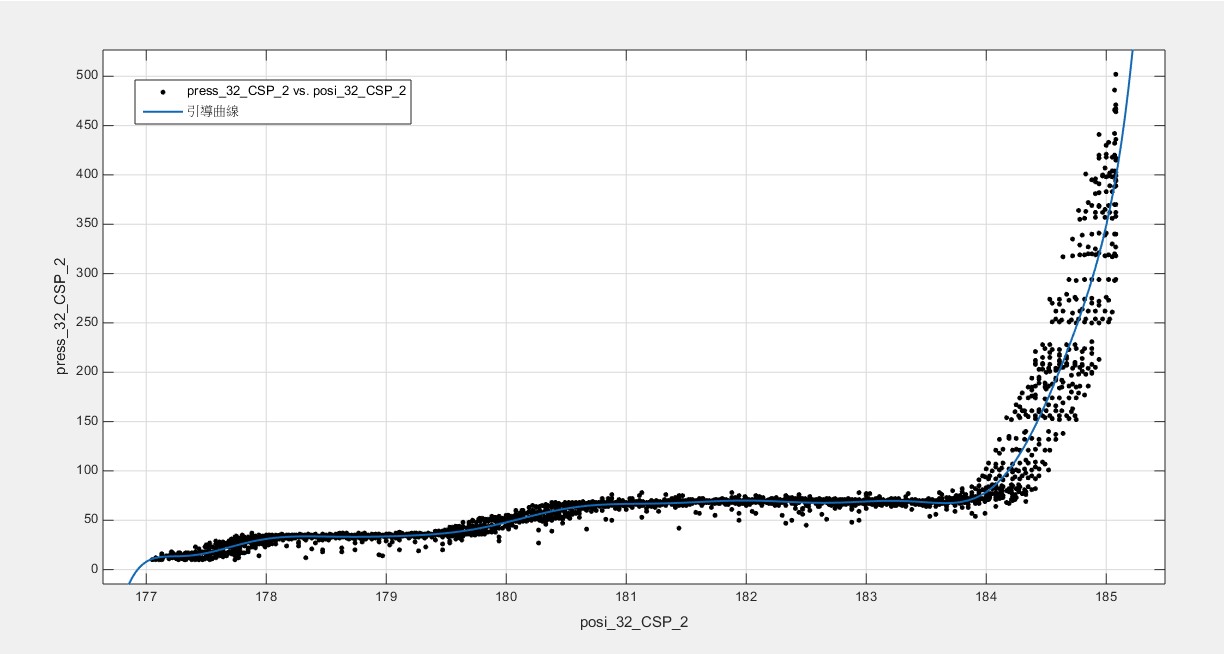(32齒輪的引導曲線 -A組2個關卡)
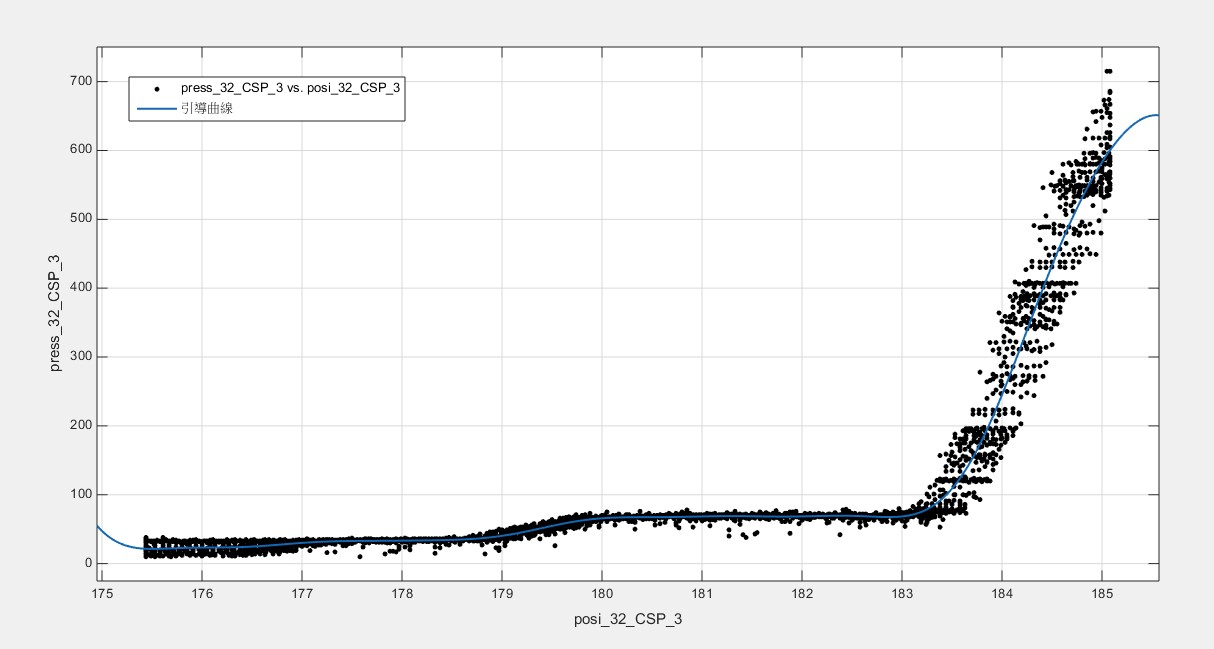(32齒輪的引導曲線 -B組3個關卡)
3.3. 基於引導曲線做基本的預警功能：
雖然壓合過程中遇到關卡，每一組的數據壓力跳躍點基本上大多不會落在這個引導曲線上面，但可以以這個引導曲線的參數化迴歸模型為雛形，在每個階段第一次跳躍的時候，進行Real Data Curve Fitting 以修正模型的參數，來檢驗下一次壓力跳躍之後是否基本上落在這個模型曲線上 - 如果向左偏離太多，代表插桿/孔洞可能斷裂變形塞住；如果向右偏離太多，孔洞或齒輪可能已經裂開⋯⋯
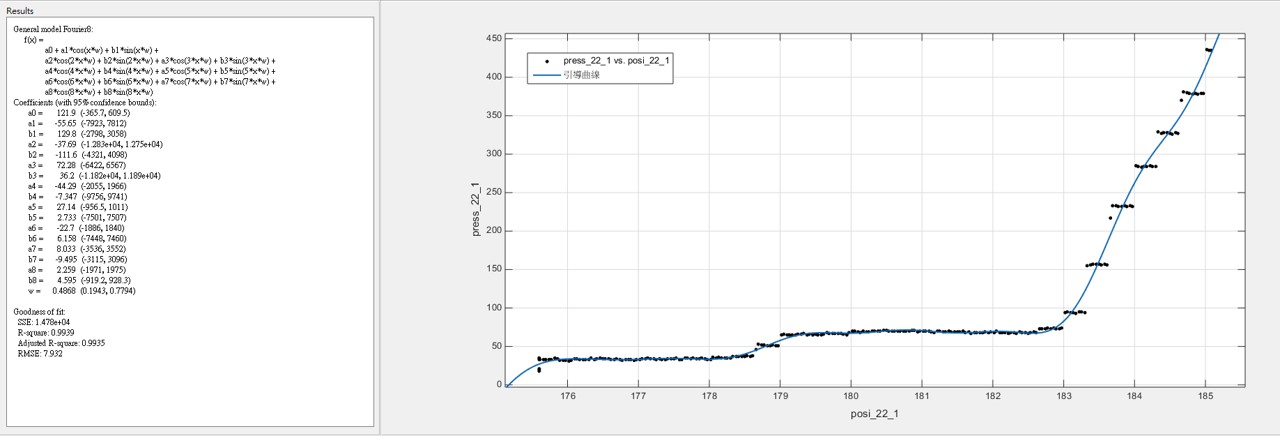
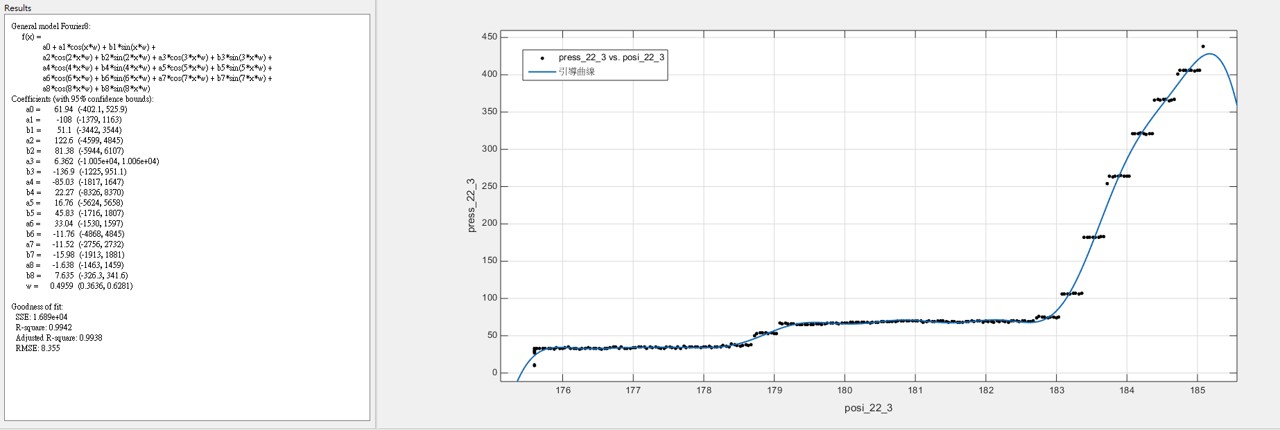
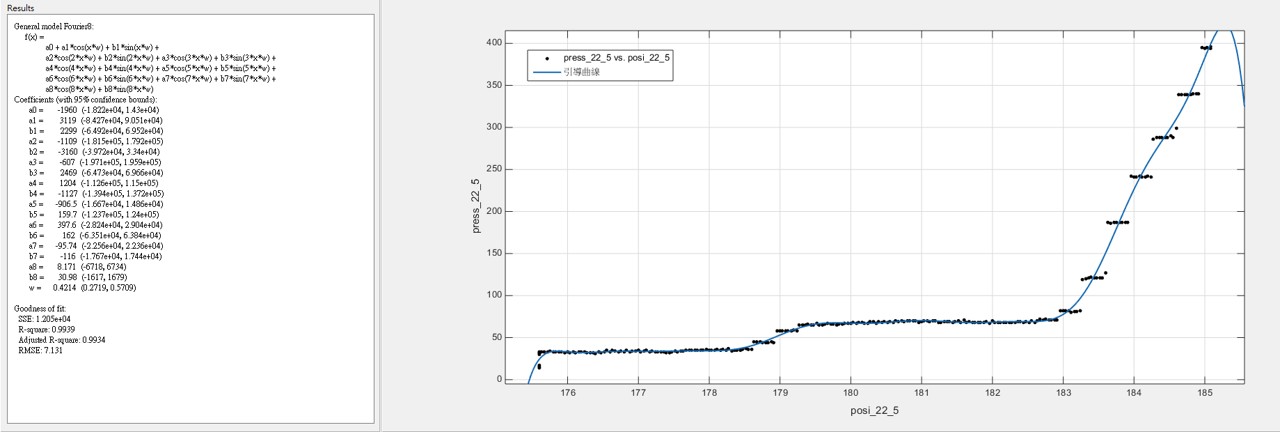
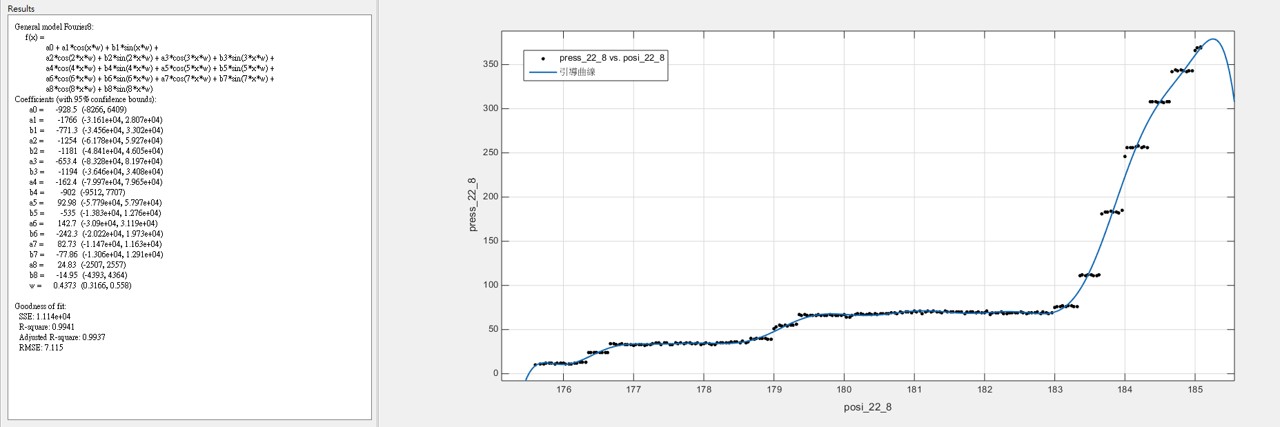
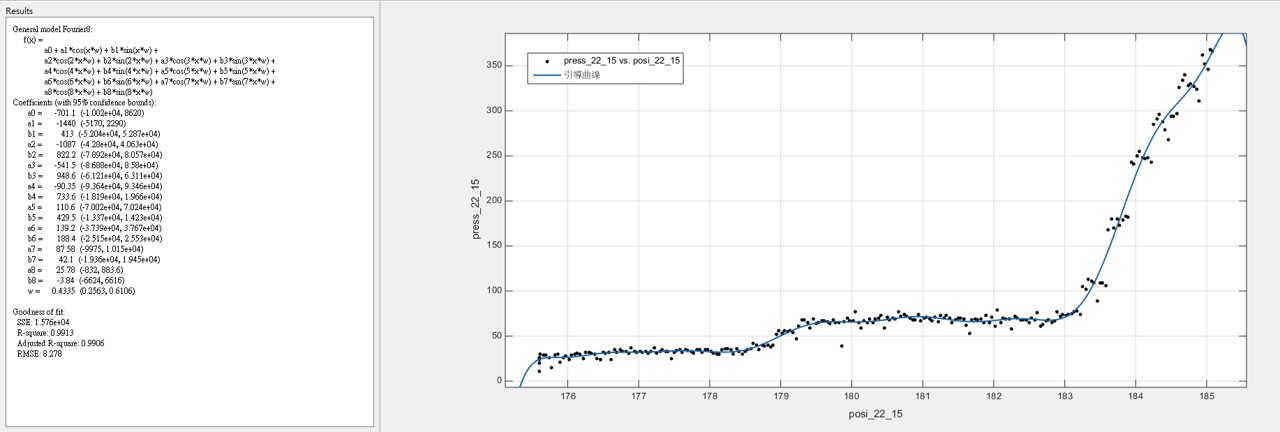
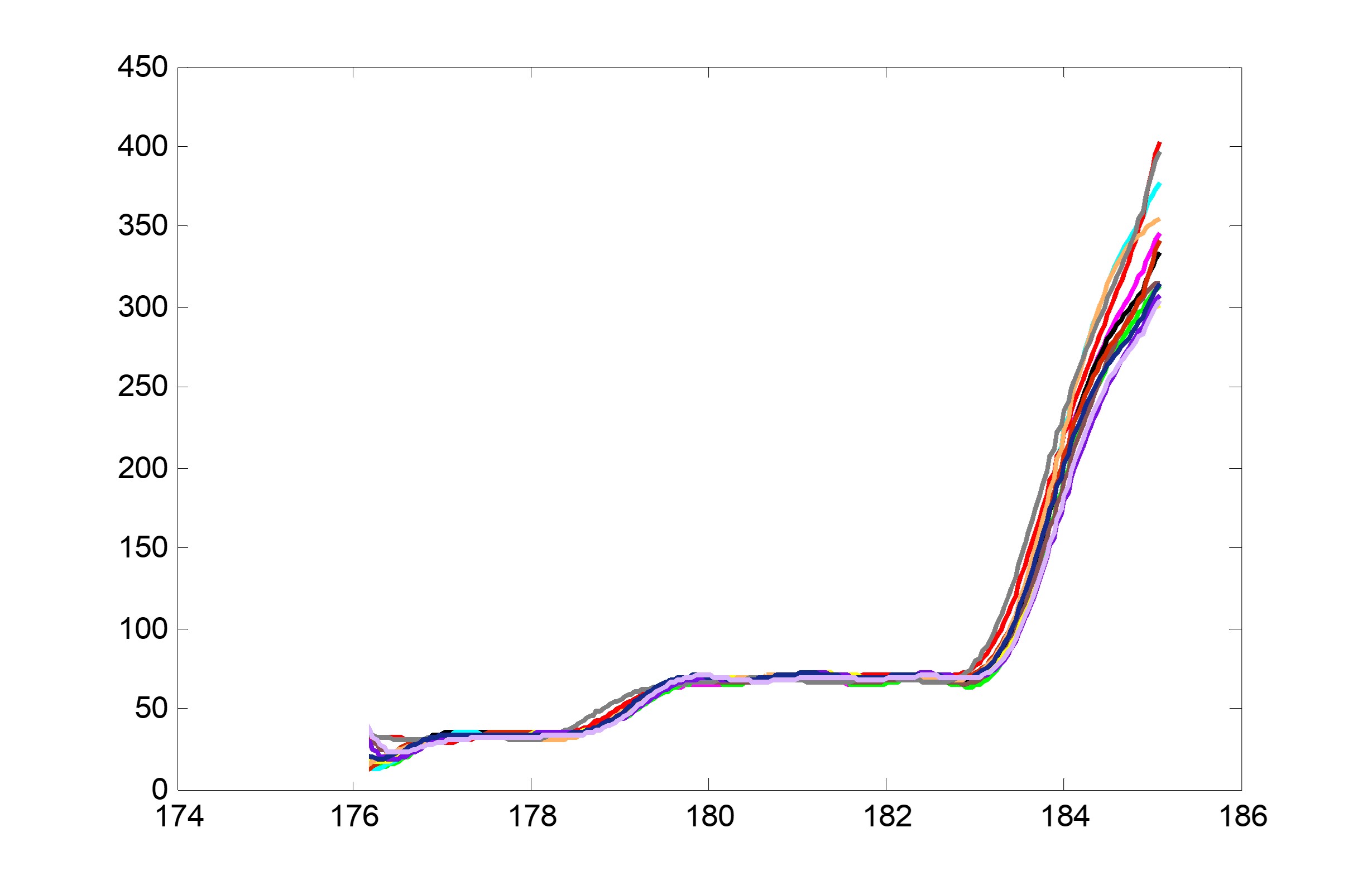
(每顆齒輪壓合過程中就會有一條它自己的曲線)
