
ChatGPT Explaning :
These documents encompass a wide spectrum of interdisciplinary topics, ranging from mathematics and computer science to signal processing and artificial intelligence. Key themes include graph theory and combinatorial topology as introduced through Euler's solution to the Seven Bridges of Königsberg problem; wavelet-based multiscale analysis and fractal geometry in modeling self-similarity, nature, and virtual environments; and remote control systems through radio channels involving RF bands, transmitter/receiver mechanisms, and encryption for interference management. They further highlight interactive learning environments, particularly in signal processing for communications, as well as the integration of AI in weapons systems. A notable mathematical highlight is the Basel problem—specifically, the solution using Parseval's identity and Fourier series. These topics are also reflected in initiatives like the TuringEuler Project at National Taipei University of Technology, collectively demonstrating the convergence of theory and application in modern science and technology.
Chatgpt 解釋 :
這些文件涵蓋了跨學科的廣泛主題,從數學與電腦科學到訊號處理與人工智慧。重點內容包括:由歐拉提出的七橋問題解法,介紹圖論與組合拓撲的基本概念;透過小波多尺度分析與碎形幾何,探索自然界的自相似現象與虛擬環境的建模;以及經由射頻(RF)頻段、發射與接收機制,以及干擾管理加密技術所構成的無線遙控系統。此外,文件也著重於互動式學習環境(特別是在通訊訊號處理方面)與人工智慧在武器系統中的應用整合。其中一項重要的數學主題是巴賽爾問題,特別是透過帕斯伐恒等式與傅立葉級數求得 的解法。這些主題也體現在如台北科技大學的 TuringEuler 計畫等專案中,整體展現了現代科學與技術中理論與應用的深度融合。
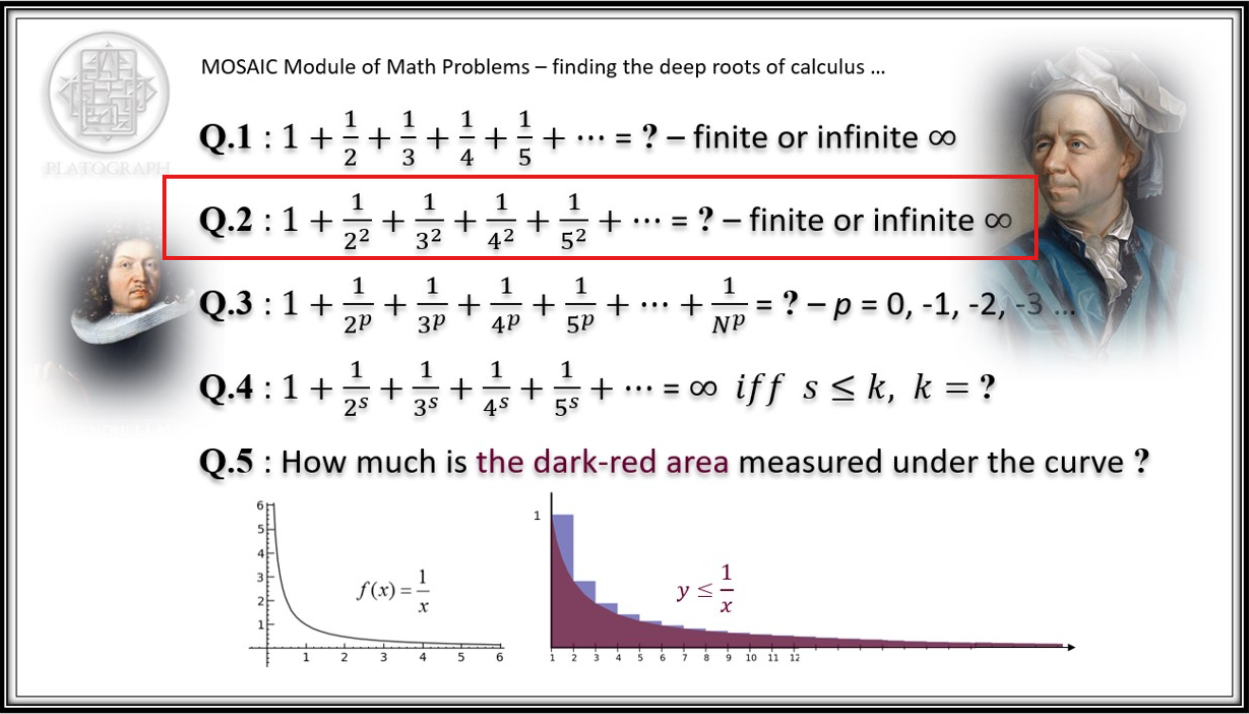
Basel 問題的解決具有深遠的數學意義,不僅僅是因為答案出乎意料,更因為它揭示了無窮級數與圓周率之間的深層聯繫。歐拉於 18 世紀初成功求出級數的確切值,此一成果解答了一個長期懸而未決的問題,首次顯示出數論與數學分析之間的緊密關係,為後來的解析數論發展奠定了基礎。
歐拉的推導方法雖不符合現代嚴謹的分析標準,但創新性與預見性令人讚嘆。他將無窮乘積與函數零點結合的技巧,為日後如傅立葉分析、黎曼ζ函數理論及解析延拓等核心領域提供了開拓性思維。Basel 問題的解決象徵著數學研究由經驗性計算邁向理論統整,並促使數學家重新思考各分支之間的本質聯繫。
更重要的是,Basel 問題所涉及的數學概念對眾多實際應用領域產生深遠影響。歐拉所使用的級數與無窮乘積觀念,後來成為傅立葉級數與傅立葉轉換的數學基礎,被廣泛應用於現代訊號處理、影像壓縮(如 JPEG)、音訊編碼、無線通訊與電子工程。另外,黎曼ζ函數的研究更是被用在量子物理、統計力學與弦論,成為數學物理中的核心工具。
從一個純粹的數學問題出發,Basel
問題的解決,改變了數學的研究方向,更透過其衍生理論影響現代科技與工程實務。此一歷史案例清楚展示了純粹數學如何為應用領域提供深層理論支持,同時也反映出數學整體發展的深度與廣度。
